Ch4: 結構化程式設計
前言
這本書是在講架構,為什麼講到範式?
與架構的關聯?
回到 Ch1.
架構:從較宏觀的角度去看
- 房子的樣貌,格局
設計: 從較微觀的角度看
- 房子的燈,插座位置
舉個前端的例子:
當收到一個 requirement....
React App Architecture:
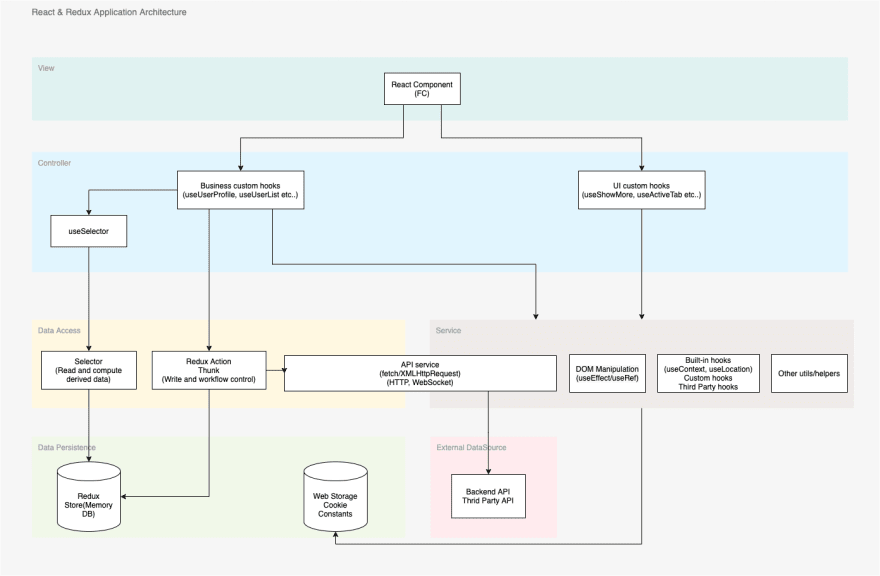
我們實際上在寫的:
// React Functional Components
// What we really write.
export const App = () => {
return <Component message="world!" />
}
export const Component = ({ message }) => {
return <h1>Hello ${message}</h1>
}
// Another Class components example
export default class App extends React.Component {
constructor(props) {
super(props)
this.state = {
// ...
}
}
render() {
return <Component message="world!" />
}
}
export default class Component extends React.Component {
constructor(props) {
super(props)
this.state = {
// ...
}
}
render() {
return <h1>Hello ${this.props.message}</h1>
}
}
範式所談論的是程式設計的方式,與語言無關。
例如 javascript 可以用 OOP,或是 FP 的方式來寫架構與設計都是整個軟體(房子)的一部份
三種範式:
- 結構化程式設計(structured programming)
- 物件導向程式設計(object-orient programming)
- 函數式程式設計(functional programming)
架構的三大關注點: 函式、元件分離、資料管理
(原文為 function,應可解釋為功能)
結構化程式設計
將一組程式拆解成一組一組小的可證明的功能,然後我們使用測試來試圖證明這些功能是不正確的。
如果測試不能證明他們是不正確的,那我們就可以認為這些功能對我們的目的來說是正確的。
歷史緣由
在早期真空管時代,電腦程式是用二進制或粗糙的組合語言編寫。使用的是紙帶或打孔卡。任何複雜的程式都包含太多細節。在看似可行的程式裡,工程師只能俯瞰一個小細節的成果,但結果常常是失敗。
Dijkstra 希望透過數學原理上的證明來解決這個問題。


證明
Dijkstra 認為可以用數學裡的層次結構來證明程式是正確的。
也就是說,程式設計師將已經證明過的結構,並將他們與程式碼綁在一起,然後自行證明他們是正確的。
goto 語句
Dijkstra 發現goto 語句的某些用法會阻止模組被分解成越來越小的單元,這樣會無法使用 divide-and-conquer的方法來合理證明。
但是有些使用方始沒有這個問題,而這些使用方式會對應到簡單的控制結構,包含:if/then/else 和 do/while。
模組如果只使用這類型的控制結構,就可以被遞迴細分為可證明的單元。
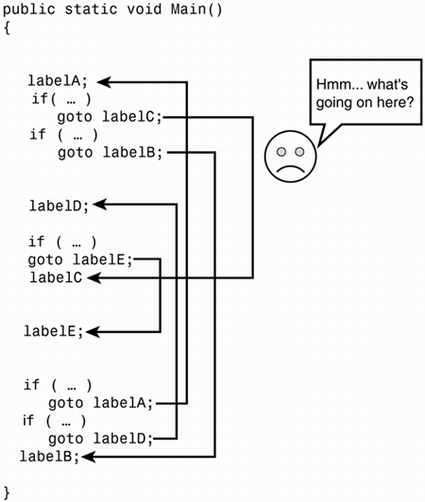

Ref: What is wrong with using goto?
與循序執行結合
Dijkstra 發現這些控制結構與循序執行結合時,是非常特殊。而
Bohm 與 Jacopini 證明了所有程式都可以使用三種結構建構出來(可以被證明),分別是:
- 循序(sequence)
- 選擇(selection)
- 迭代(iteration) (網路查是遞迴,迴圈)
原文:建構可證模組的控制結構就是可建構所有城市的控制結構的最小集合,因此結構化程式設計誕生了。
換句話說: 所有程式的可以由很多個小的可以被證明的程式所組成。
| 循序結構 | 選擇結構 | 迭代結構構 |
|---|---|---|
結構化程式設計的證明
- 循序(sequence)
- 透過簡單來列舉: 由循序輸入追蹤到循序輸出。
- 選擇(selection)
- 使用列舉來證明: 將選擇的每條路徑都列舉出來,如果兩條路徑最終都產生了恰當的數學結果,則證明就是可靠的。
- 迭代(iteration)
- 使用數學歸納法: 先透過列舉證明 1 的情況,然後再次透過列舉,證明如果 N 假定是正確的,那麼 N+1 就是正確的。
大型程式功能分解
因為結構化程式設計允許將模組分解成一個個的可證明的單元,所以只要程式設計師遵循這些限制規則(參考 goto),
就可以將大型的系統,分解成一個個微小的、可證明功能的模組和元件。
現在,我們都是結構化的程式設計師,雖然這不一定是你選擇的。
只是因為我們的語言無法讓我們選擇使用無條件直接轉移控制。 (really? 😏😏😏)
科學的證明與測試
數學是要證明陳述是 true,科學是要證明陳述是 false
科學的證明
科學的定理和定律都無法用證明來表達其正確性。
例如:證明牛頓第二運動定律 F=ma,無倫多少次實驗,總有一些實驗證明他是不正確的。
- 科學並非要證明陳述是正確的,而是要證明陳述是錯誤的。
- 如果我們經過努力還是無法證明他是 false,那麽我們就認為他足夠正確。
測試
現在我們的測試都是用科學的方式證明
- 測試顯示了錯誤的存在,而不是沒有錯誤。
- 這種證明不正確的方式只能用於可證的程式,一個不可正的程式(無限制的使用 goto)不能被認為是正確的。
測試的問題
// javascript
function Add(a, b) {
return a + b
}
// safe?
test('Is sum of two number', () => {
expect(Add(2, 2).toBe(4)
})
你永遠不知道User會怎麼使用我們的產品

總結
- 無限制使用
goto會使程式無法被分解成可被證明的單元(無法被測試) - 使用結構化程式迫使我們將程式分解成一組組可被證明的單元
- 大型程式由小的可被測試的單元組成
- 回到開頭